그래프 탐색이나 기타 새로운 알고리즘 문제에 도전하고 싶은데 다른 공부도 할 게 너무 많아 원래 알던 범위에서 빙글빙글 돌며 양치기나 하고 있다.. 이러다가 6개월 내내 백준 실버 프로그래머스 1레벨 문제만 풀고 있는 건 아니겠지..?
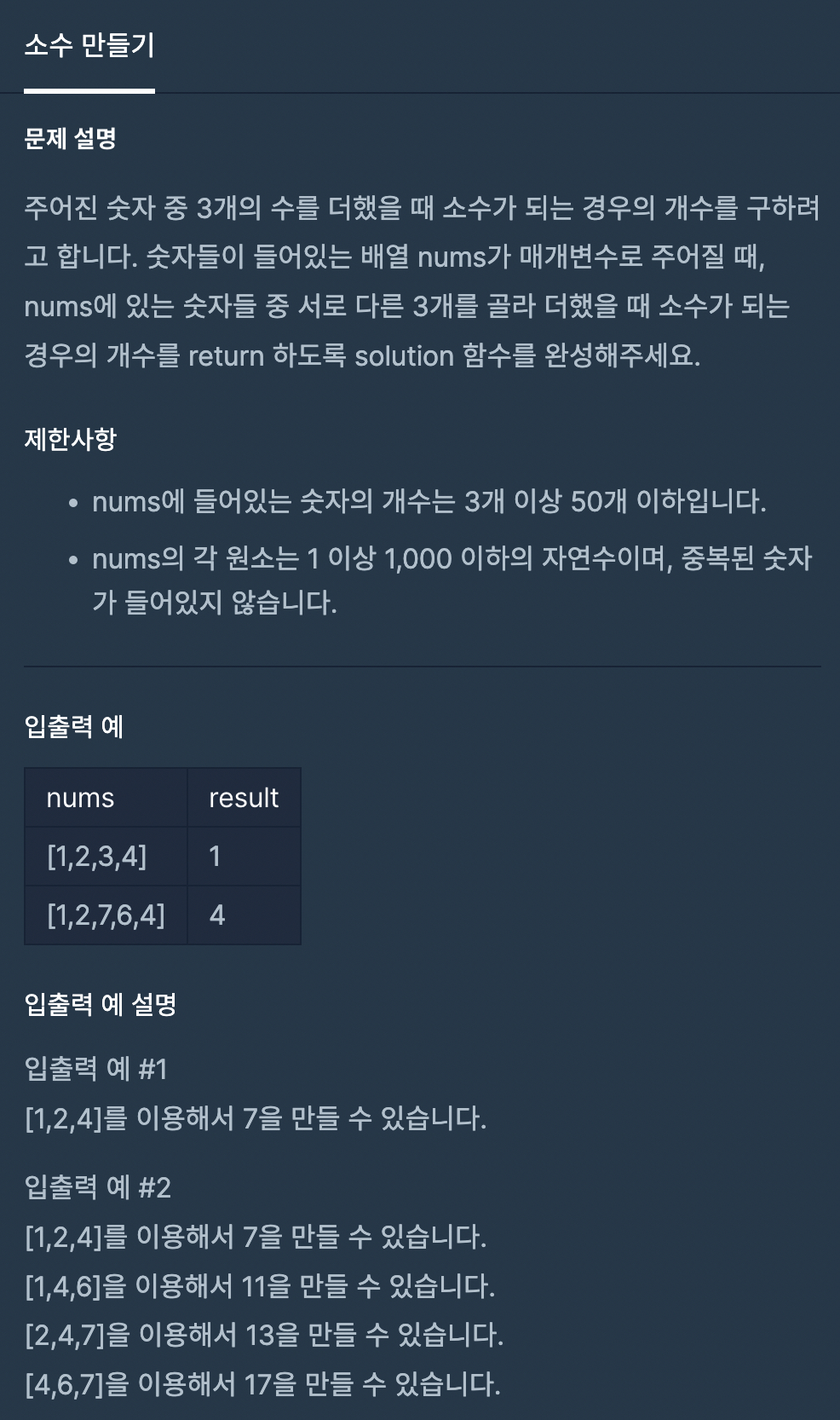
쩝.. 아무튼 오랜만에 만난 소수 구하기 문제이다.
https://7357.tistory.com/104?category=1065986
0부터 n까지의 수 중 소수 구하기 : 에라토스테네스의 체
고대 그리스 수학자 에라토스테네스가 발견한 소수를 구하는 간편한 방법이다. 알고리즘 중에 그나마 쉬운 편에 속한다. (1) 우선 0과 1은 소수가 아니기때문에 제외한다. (2) 소수인 2를 제외한 2
7357.tistory.com
몇 번째 우려먹는 건지 모르겠지만 저난이도의 소수 관련 문제는 에라토스테네스 체 하나면 떡을 치니까 알아두도록 하자.
이번 문제는 해당 링크에서 사용했던 방법을 그대로 적용한 풀이 방법(미리 배열 생성해서 소수 구해놓기)과 그 때 그 때 주어진 숫자로 소수인지 판별하는 방법 두 가지를 모두 시도해보고 유의미한 시간차가 있는지 확인해보았다.
1. 미리 소수를 모두 구해놓은 다음 판별하기
import java.util.*;
class Solution {
public static boolean[] isCompositeNum = new boolean[3001];
public int solution(int[] nums) {
findCompositeNum();
int length = nums.length;
int result = 0;
for (int i=0; i<length-2; i++) {
for (int j=i+1; j<length-1; j++) {
for (int k=j+1; k<length; k++) {
int sum = nums[i]+nums[j]+nums[k];
if (!isCompositeNum[sum]) {
result+=1;
}
}
}
}
return result;
}
public static void findCompositeNum() {
isCompositeNum[0] = isCompositeNum[1] = true;
for (int i=2; i*i<=isCompositeNum.length; i++) {
if ( !isCompositeNum[i]) {
for (int j=i*i; j<=isCompositeNum.length; j+=i) {
isCompositeNum[j] = true;
}
}
}
}
}3중 for문이 들어가는 건 둘 다 똑같다.
단 3중 포문에 i=0; j=i+1; k=j+1로 시작하게 만들어 자기 자신을 더하는 일이 없도록 한다.
나는 가끔 실수할 때가 있는데, k를 i+2가 아니라 j+1로 두어야 한다. 둘은 전혀 다르다.
그렇게 합계를 구한 뒤 미리 만들어놓은 boolean배열에서 해당 값이 소수인지 아닌지 확인하고 소수라면 결과값에 1을 더한다.
해당 배열을 만드는 방법은 위 링크에 상세하게 설명해놨으므로 생략한다.
배열 크기가 3001인 이유는 각 원소가 1 이상 1000 이하의 자연수이기 때문이다.
정확히 따지자면 중복이 안되기 때문에 1000 + 999 + 998 + 1 = 2998의 크기로 만들어주면 된다.
결과는 이렇게 나왔다.
2. 각 합계마다 소수를 판별하는 방법.
import java.util.*;
class Solution {
public int solution(int[] nums) {
int length = nums.length;
int result = 0;
for (int i=0; i<length-2; i++) {
for (int j=i+1; j<length-1; j++) {
for (int k=j+1; k<length; k++) {
int sum = nums[i]+nums[j]+nums[k];
if (sum%2==0 || sum%3==0) {continue;}
result += (isPrimeNum(sum)) ? 1 : 0;
}
}
}
return result;
}
public static boolean isPrimeNum(int num) {
for (int i=5; i*i<=num; i+=2) {
if (num%i==0) { return false; }
}
return true;
}
}
배열을 사용하지 않는다는 것을 제외하면 위와 거의 동일하다.
isPrimeNum 메서드는 i j k의 합계를 인자로 받아 해당 수의 약수가 있는지 구한다.
이 때 메서드에 들어가기 전에 2와 3을 약수로 가지는 숫자는 미리 걸러낸다.
여기서 얼마나 걸러낼지는 본인 마음대로 하면 된다. 난 2와 3 정도만 걸러내도 남는 수가 거의 없다고 판단해서 이렇게 만들었다.
아마 손으로 일일히 걸러내도 큰 차이는 없을 것으로 예상된다.
그리고 소수를 구할 때 짝수는 이미 %2에서 모두 걸러냈으므로 홀수에서 시작해서 +2씩 더한다.

굳이 3000까지의 소수를 모두 구하는 방식보다 2번 방법으로 푸는 게 더 빠르지 않을까 생각했었는데 별반 차이가 없었다.
오히려 2번이 느린 테스트 케이스도 있는 걸 보면 아마 각 합계가 꽤나 큰 경우였을 것 같다.
'CS ﹒ Algorithm > Programmers' 카테고리의 다른 글
| 프로그래머스 문제풀이 (6) 성격 유형 검사하기 (0) | 2022.08.19 |
|---|---|
| 프로그래머스 문제풀이 (5) 키패드 누르기 (0) | 2022.08.17 |
| Java 프로그래머스 문제풀이 (4) 없는 숫자 더하기 (0) | 2022.08.11 |
| 프로그래머스 문제 풀이 (2) 완주하지 못한 선수 (0) | 2022.07.24 |
| 프로그래머스 문제풀이 (1) 폰켓몬 (0) | 2022.07.21 |



