관련이 있는 문제라서 두 개를 연달아 풀었다.
4번은 1차원 배열 구간합이라서 엄청나게 쉽고, 5번은 풀어본 경험이 있거나 머리 속에서 그림이 그려지는 사람이 아니라면 어려울 수 있다.
우선 구간 합 알고리즘이 필요한 이유는 필요할 때마다 합을 구하는 것보다 미리 누적값으로 표를 만들어놓고 가져오는 것이 효율적이기 때문이다.
만약 2차원 배열에서 매번 구간합의 구하면 O(NM)의 시간복잡도를 가지게 되지만 구간합을 미리 구해놓고 값을 꺼내오기만 한다면 O(1)로 해결되기 때문에 당연히 엄청난 차이가 날 수 밖에 없다.

크게 설명할 게 없다.
미리 더해놓고 필요할 때 꺼내되, 해당 구간에 속하지 않는 부분을 제거해주면 된다.
즉, 1차원 배열에서 구간합을 구하는 공식은 배열[x2] - 배열 [x1-1]이다.
너무 쉬운 부분이라 설렁설렁 넘어가겠다. 안 풀어봤으면 직접 풀어보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int arrLength = Integer.parseInt(st.nextToken()); // 받을 숫자의 개수
int count = Integer.parseInt(st.nextToken()); // 누적합 구할 횟수
int[] sumArr = new int[arrLength];
int sum = 0; // 누적합 계산용 변수
st = new StringTokenizer(br.readLine(), " ");
for (int i=0; i<arrLength; i++) {
int num = Integer.parseInt(st.nextToken());
sum += num; // 반복시마다 누적해서 대입
sumArr[i] = sum;
}
StringBuilder result = new StringBuilder();
for (int i=0; i<count; i++) {
st = new StringTokenizer(br.readLine(), " ");
int index1 = Integer.parseInt(st.nextToken())-1;
int index2 = Integer.parseInt(st.nextToken())-1;
if ( index1 != 0 ) {
result.append(sumArr[index2] - sumArr[index1 - 1]).append("\n");
} else result.append(sumArr[index2]).append("\n");
}
System.out.println(result.toString());
}
}
|
cs |
너무 대충 풀어서 if (index!=0) ~부분이 조금 아쉬운데,
애초에 배열을 한 칸 더 크게 만들어서 0번 인덱스를 비워버리면 인덱스에 1씩 빼주지 않아도 되고 조건문도 작성하지 않아도 되기 때문에 가독성이 좋아진다.
다음 문제는 해당 부분을 고려해서 풀었다.
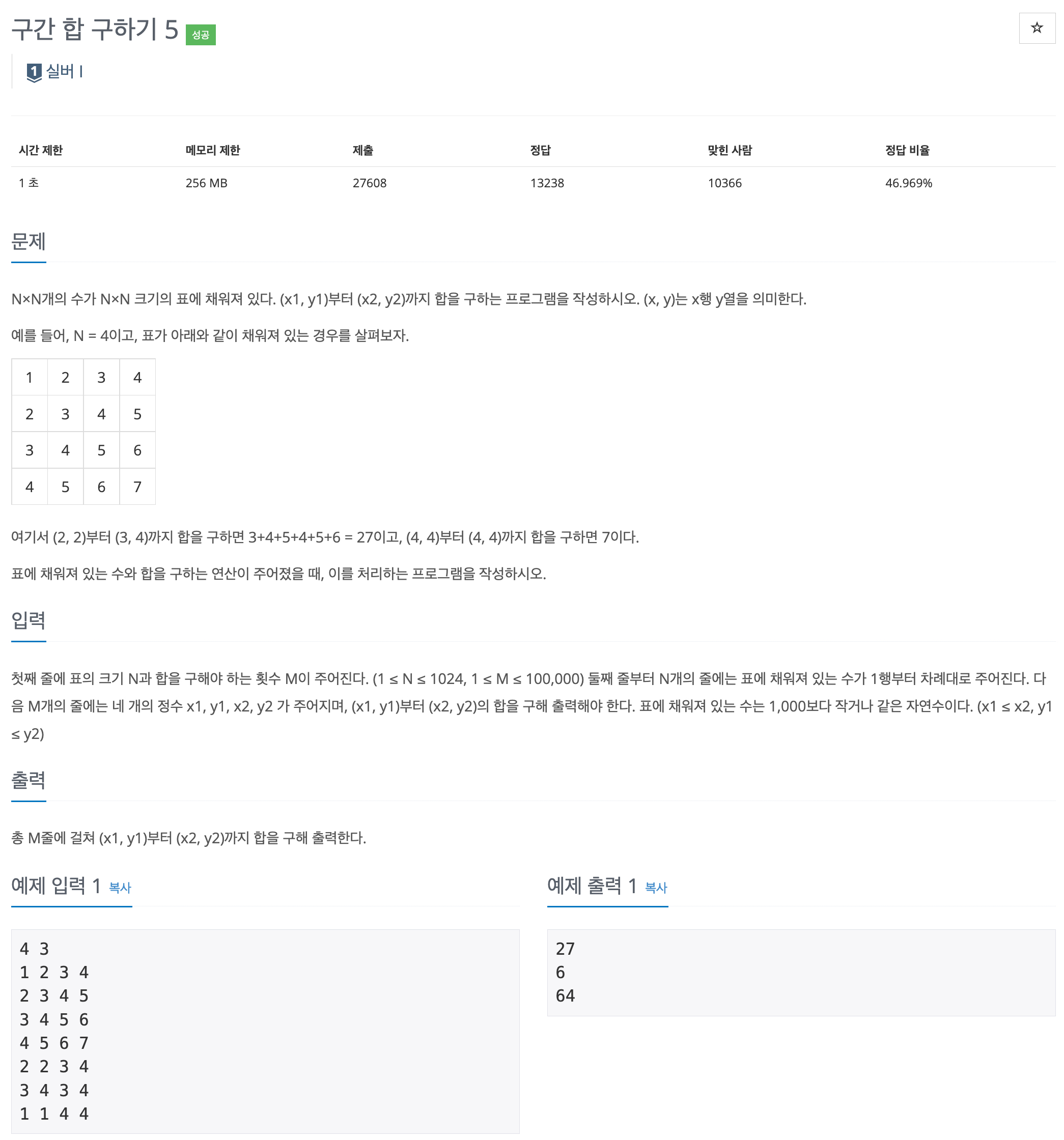
솔직히 엄청나게 쉽게 생각했는데, 꽤나 고전했다.
2차원 배열이 머리속에서 짜자잔~하고 펼쳐지는 사람이라면 쉽게 풀 수 있는 문제다.
(2,2)부터 (3,4)까지의 합을 구하면 3+4+5+4+5+6이라고 한다.
음.. 이런 식으로 구하는 거구만
일단 잘 모르겠으니 해당 규칙에 의거하여 표를 그려보자

글씨는 양해 바랍니다..🥲
해당 표를 보면 한 가지 규칙을 알 수 있다.
우선 (2,2)에 위치한 구간합인 8을 보자.
(1)(2)
(2)(3)
중 3의 위치에 8이 온 것인데, 이는 2+2+3+1과 같다.
그리고 구간합 그린 표 기준으로는
(1)(3)
(3)(8)
3(구간합)+3(구간합)+3(원래 2,2위치에 오는 수)-1과 같다
(2,3)위치의 15를 보자.
(3)(8)
(6)(15)
8 + 6 + 4(원래 해당 위치에 오는 수) - 3 = 15가 나오고 있다.
즉 해당 공식을 이용하면 우리가 입력값을 받아 즉시 구간합 배열로 만들어줄 수 있다는 것을 의미한다.
이 문제에서 각 위치의 누적합을 구하는 공식은
구간합배열[x][y] = 구간합배열[x-1][y] + 구간합배열[x][y-1] - 구간합배열[x-1][y-1] + 원래 입력 받을 값이다.
여기서 "헉.. 근데 그럼 0번 인덱스면 어떡해요?? 전부 조건문 처리해요??"라고 생각할 수 있다.
위에서 말했듯 애초에 배열을 +1 크기로 만들고 0번 배열은 비워주면 손쉽게 해결할 수 있다.
그러면 이제 각 위치의 (0,0)~(x,y) 구간합을 구하는 것은 해결했다. (정확히 말하자면 이건 부분합이다)
이제 범위 구간합만 구하면 된다.
다시 문제에서 준 예시를 보자.

(2,2) (3,4)가 노란색 구간, 하늘색(민트색?)이 제외해야하는 구간, 초록색은 하늘색 구간에서 중복으로 빠지는 구간이다.
이 그림을 바탕으로 계산해보면 42-10-6+1 = 27이 나온다.
드디어 (x1,y1)부터 (x2,y2)까지의 구간합을 구하는 공식을 얻을 수 있게 되었다..
혹시 아직 안 풀어봤으면 구간합을 구하는 공식은 직접 구해보자.
여기까지 봤으면 이미 정답을 본 것이나 마찬가지다.
공식과 정답은 밑으로 조금 더 내리면 볼 수 있다
2차원 배열의 (x1,y1) ~ (x2,y2) 구간합을 구하는 공식
구간합배열[x2,y2] - 구간합배열[x2,y1-1] - 구간합배열[x1-1,y2] + 구간합배열[x1-1, y1-1]이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[][] arr = new int[N+1][N+1];
int sum = 0;
for (int i=1; i< arr.length; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j=1; j<arr[i].length; j++) {
int input = Integer.parseInt(st.nextToken());
arr[i][j] = arr[i-1][j] + arr[i][j-1] + input - arr[i-1][j-1];
}
}
StringBuilder sb = new StringBuilder();
for (int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine(), " ");
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int result = arr[x2][y2] - arr[x2][y1-1] - arr[x1-1][y2] + arr[x1-1][y1-1];
sb.append(result).append("\n");
}
System.out.println(sb.toString());
}
}
|
cs |
'CS ﹒ Algorithm > Baekjoon' 카테고리의 다른 글
| Java 백준 문제풀이 (40) 2018번: 수들의 합5 (0) | 2022.09.09 |
|---|---|
| Java 백준 문제풀이 (39) 10986 : 나머지 합 (0) | 2022.09.08 |
| Java 백준 문제풀이 (37) 1085, 3009, 4153, 3053 쉽지만 어려운 문제 4종세트 (0) | 2022.08.09 |
| Java 백준 문제풀이 (36) 연산자 끼워넣기 (0) | 2022.08.06 |
| Java 백준 문제풀이 (35) 15651: N과 M (3) (0) | 2022.08.03 |



