푸는 방법만 알면 거저먹는 문제지만 나는 푸는 방법을 몰라서 조금 헤맸다.
그래도 처음 풀어보는 플래티넘 문제인데 검색할 필요가 없었으니 어지간한 골드 문제보다 쉬웠던 것 같다.
오늘부터는 내가 처음 생각하고 시도하고 틀린 과정, 그리고 잘못 작성했던 주석까지 모조리 올리기로 했다.
이렇게 하면 남들한테 보여줘야하는 것이니 부끄러워서라도 과정 건너뛰지 않고 조금 더 차근차근 풀 수 있지 않을까 싶어서..
그리고 풀이를 보는 사람도 나처럼 실력이 부족한 사람들은 정답만 보는 것보다 시행착오까지 보는 게 더 도움이 되지 않을까 싶다.
우선 나는 항상 문제의 조건을 읽으면서 바로바로 해당 요구사항을 어떻게 풀이에 적용할지 주석으로 작성한다.
내가 코드 작성 전 작성한 주석은 다음과 같다.
// N개의 수로 이루어진 수열
// 버블소트 수행 시 swap이 발생하는 횟수 체크하는 프로그램 작성
// N의 최대 개수 500,000
// 버블소트로 연산 시 O(n^2) => 250000000000
// 머지소트로 연산 시 O(nlog(n)) => 2849485
// 일반적으로 초당 연산 가능 횟수 -> 1억~10억
// -> 다른 방법도 있겠지만 일반적으로 저격이 어려운 merge sort로 풀자.
// A[i]의 최대 범위 = 1,000,000,000 -> int 범위가 어디까지였지..? 일단 long 쓰자
// 수의 위치가 바뀌는 경우마다 count를 해줘도 머지소트는 한 번에 여러 인덱스를 건너뛰니까 의미가 없다.
// [r]-[l]로 계산하면 되려나..? 일단 {3,2,1}일 때는 충분히 가능하다.내가 생각한 풀이 조건
1. 버블소트 수행 시 swap이 발생하는 횟수를 체크하는 프로그램을 작성해야 하는데, N의 최대 개수가 500,000개다.
그런데 버블소트의 시간복잡도는 O(n^2)로 최대 250000000000번의 연산이 필요하다.
일반적으로 초당 연산 가능횟수를 최소 1억, 최대 10억 정도로 잡는데 문제에서 제시하는 1초의 시간으로는 O(n^2) 시간 복잡도를 가진 알고리즘은 절대 적용할 수 없다.
반면, O(nlogn)의 알고리즘 사용 시 2849485번만에 연산이 가능하므로 1초면 차고 넘친다.
O(nlogn)의 정렬 알고리즘은 대표적으로(내가 구현할 수 있는 것들이 ㅎㅎ;) 퀵 정렬, 병합 정렬이 있으나 퀵 정렬은 테스트케이스에 저격당하기 쉬워서 시도하지 않는 것이 정신 건강에 이로울 것이라고 생각했다.
따라서 병합 정렬을 택했다.
2. 이제 배열에서 수의 위치가 바뀌는 경우를 count해주는 방법만 구하면 된다. 아래에 내가 발로 그린 그림을 보면 알겠지만, buble sort는 인덱스 한 칸씩 수가 움직이는 굉장히 비효율적인 알고리즘인데 merge sort에서는 한 번에 여러칸을 건너뛰기 때문에 이것을 어떻게 구할지가 문제였다.
그다지 어려운 건 아닌 것 같지만 당장 내 작은 뇌로 생각할 수 있는 풀이법은 merge sort에서 arr[left]가 arr[right]보다 클 때, rigth-left만큼의 값을 count에 더해주는 것이였다.
실제로 {3, 2, 1}배열의 경우 해당 방법으로 3이라는 답이 나온다.
그리고 틀렸다.
틀리고나서 내가 뭔가 잘못했나 싶어서 그림으로 그려봤다.
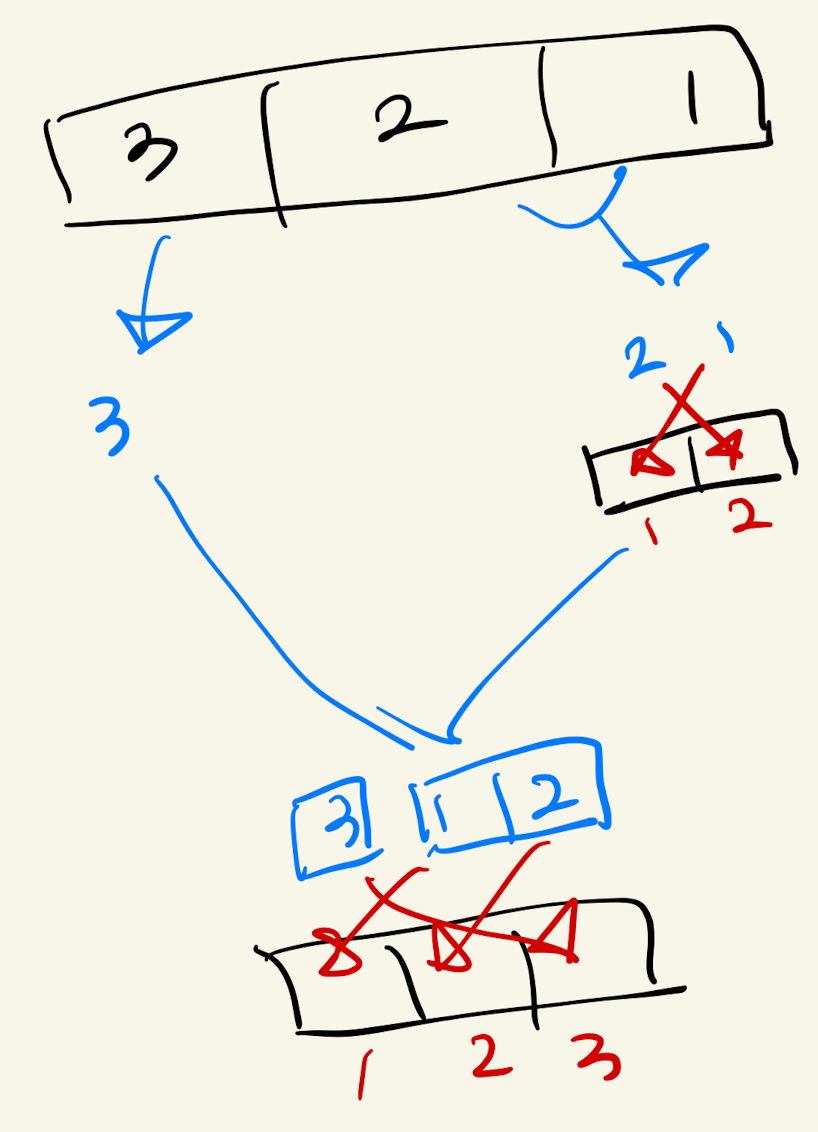
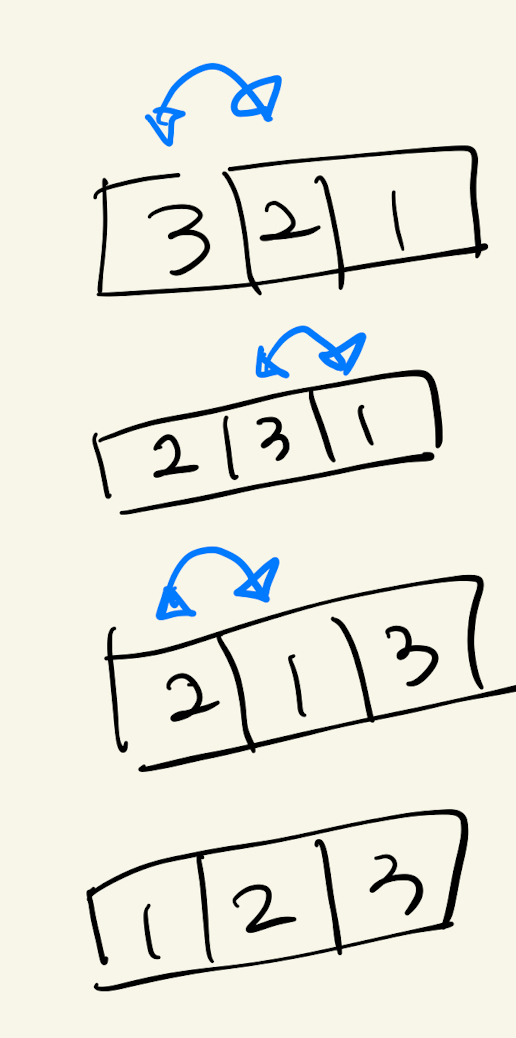
맞는 것 같은데 왜 안될까? 반례를 찾아봐야 한다.

맞잖아!!!!!! 맞잖아!!!!! 맞잖아!!!!!!
라고 할 때 쯤 반례를 찾을 수 있었다.

7 4 5 1 3이 들어갔을 때 8이 나와야하는데, 내 코드에서는 9가 나온다.
뭔가 잘못됐다.
이것 외에도 몇 가지 테스트를 해봤는데, 특정 조건에 따라 정답이 1씩 크게 나온다.
그래서 위 반례로 디버깅을 돌려봤다.
count가 더해지는 과정은 아래와 같았다.
{4. 7} +1
{4, 5, 7} +1
=> 이후 {1,3}과 합쳐짐
{1,5,7,4,3} +3
{1,5,7,3,4} +4
??
이 부분에서 엄청나게 방황했는데 결국 (다행히 스스로) 이유를 알아낼 수 있었다.
기준점이 변하면 안된다.
r, 즉 m+1에서 l을 빼겠다는 생각까지는 좋았다. 이유가 잘못됐을 뿐.
문제는 한 번의 while문에서 두 번의 교환이 일어날 경우
r이 ++된 상태이기 때문에 이동해야하는 수(count)가 실제보다 1 더 증가한다.
보기엔 그럴듯한 전제조건이였지만 근거가 잘못됐기 때문에 이 사단이 났다는 뜻이다.
이건 병합 정렬에 대한 내 이해도 부족 때문에 일어난 문제다.
병합 정렬이 무엇인지 다시 한 번 생각해보자.
병합 정렬에서 각 배열은 이미 정렬되어 있는 상태다.
예를 들어 {4, 7}, {2, 5, 8} 이런 식으로 만나지 {7, 4}, {2, 8, 5} 이렇게 만날 일이 절대 없다.
즉, 우리가 체크해야할 부분은 단순히 r-l로 이동한 총 인덱스 수를 세는 것이 아니다.
중간 지점을 기준으로 좌측 배열에 있는 해당 수 arr[l]보다 작은 수 개수를 세야하는 것이다.
버블 소트가 동작하는 모습을 머리속으로 그려보면 무슨 말인지 이해가 될 것이다.
예를 들어 {4,7} {2,5,8}이 만났을 때, {2,4,5,8,7}의 형태가 된다
여기서 4와 7이 버블소트 시 움직이는 횟수를 어떻게 쉽게 구할 수 있을까?
그냥 좌측에 있는 수보다 작은 수가 우측에 있을 경우 해당 경우의 수를 모두 체크하면 된다.
4는 2보다 크니 +1
7은 2, 5보다 크니 +2로 총 3번 움직인다.
이걸 mergesort에서 어떻게 구할 수 있을까?
{4,7} {2,5,8}이 있을 때
2가 가장 작으므로 2가 먼저 배열에 들어간다.
그리고 l에는 더 큰 수 2개가 있으니 2를 더한다.
그 다음 4가 배열에 들어가고 더해지는 수는 없다.
그 다음 5가 배열에 들어가고 좌측 배열에는 더 큰 수 1개가 있으니 1을 더한다.
이후 7, 8이 배열에 들어가고 더해지는 수는 없으며 결과는 3이다.
이를 코드로 나타내면 다음과 같다
if ( arr[l] > arr[r] )
count = count + m+1( 우측 배열의 시작지점 ) - l(좌측배열의 해당 수 인덱스)
temp[index++] = arr[r++];
1. l = 0, r = 2;
count = 0 + 2 - 0;
count = 2;
2. l = 0, r = 3; x
3. l = 1, r = 3;
count = 2 + 2 - 1;
count = 3;
4. 이후 생략
아무튼 어떻게든 혼자 풀었다.
코드는 처음 주석 작성했던 것을 지우지 않고 그냥 뒀으니 주석은 신경쓰지 말자. 틀린 전제가 적혀있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
|
import java.util.*;
import java.io.*;
public class Main {
static long count = 0;
public static void main(String[] args) throws Exception {
// N개의 수로 이루어진 수열
// 버블소트 수행 시 swap이 발생하는 횟수 체크하는 프로그램 작성
// N의 최대 개수 500,000
// 버블소트로 연산 시 O(n^2) => 250000000000
// 머지소트로 연산 시 O(nlog(n)) => 2849485
// 일반적으로 초당 연산 가능 횟수 -> 1억~10억
// -> 다른 방법도 있겠지만 일반적으로 저격이 어려운 merge sort로 풀자.
// A[i]의 최대 범위 = 1,000,000,000 -> 헷갈리니까 일단 long 자료형을 쓰자 (ㅋㅋ 응 아니야~ int 20억까지 커버됨)
// 수의 위치가 바뀌는 경우 (left가 right보다 큰 경우) 마다 카운트를 ++해주면 될 듯?
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
long[] arr = new long[N];
long[] temp = new long[N];
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for (int i = 0; i < N; i++) {
arr[i] = Long.parseLong(st.nextToken());
}
mergeSort(arr, 0, arr.length-1, temp);
System.out.println(count);
}
public static void mergeSort(long[] arr, int left, int right, long[] temp) {
if (left != right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid + 1, right, temp);
merge(arr, left, right, temp);
}
}
public static void merge(long[] arr, int left, int right, long[] temp) {
int m = (left + right) / 2;
int l = left;
int r = m + 1;
int i = left;
while (l <= m && r <= right) {
if (arr[l] > arr[r]) {
count += (m-l+1);
temp[i++] = arr[r++];
} else {
temp[i++] = arr[l++];
}
}
// 만약 l이 r보다 크다면
// r++ index++
// count++
// else
// l++ index++
if (l > m) {
while (r <= right) {
temp[i++] = arr[r++];
}
}
// 만약 l이 m보다 크다면
// index가 가득찰 때까지 r++
if (r > l) {
while (l <= m) {
temp[i++] = arr[l++];
}
}
// else
// 만약 r이 l보다 크다면
// index가 가득찰 때까지 l++
for (int j = left; j <= right; j++) {
arr[j] = temp[j];
}
// arr에 temp 값 저장
}
}
|
cs |
'CS ﹒ Algorithm > Baekjoon' 카테고리의 다른 글
| Java 백준 문제풀이 (52) 2023_신기한 소수 (2) | 2022.10.12 |
|---|---|
| Java 백준 문제풀이 (51) 연결 요소의 개수 (3) | 2022.10.09 |
| 백준 문제풀이(49) 수 정렬하기2 병합정렬 (0) | 2022.10.02 |
| JAVA 백준 문제풀이 (48) ATM (0) | 2022.09.27 |
| Java 백준 문제풀이 (47) 버블 소트 (0) | 2022.09.24 |



