
첫 달에는 새로 태어난 토끼 한 쌍만 존재한다.
두 달 이상이 된 토끼는 번식 가능하다.
번식 가능한 토끼 한 쌍은 매달 새끼 한 쌍을 낳는다.
토끼는 죽지 않는다.
10개월째에 총 몇 쌍의 토끼가 존재하는가?
사각형 채우기나 귓바퀴 예제보다는 토끼가 제일 와닿는 예시인 것 같다.
나는 사칙연산 이외의 수학을 사용해보지 않은지 10년이 넘은 사람이라 공식을 봐도 무슨 말인지 잘 이해되지 않아서 아래의 정의만 보고 코드를 작성했다.

F[0] = 0;
F[1] = 1;
F[n] = F[n-1] + F[n-2];
어? 익숙하다.
누가봐도 코드에 갖다 붙이기 좋은 형태다.
// 배열 활용 예시
public static int fibonacci(int num) {
int[] arr = new int[num];
int result = 0;
// F0은 인덱스가 아니라 실제로 0이 대입됐을 경우를 말하는 것이기 때문에 num을 +1해주거나 혹은 생략
arr[0]=1; // F1 = 1;
arr[1]=1; // F2 = 1;
// n-2의 공식을 작성해야 하므로 arr[1]까지는 미리 정의해줘야 한다.
for (int i=2; i<arr.length; i++) {
arr[i]=arr[i-1]+arr[i-2];
}
return arr[arr.length-1];
}
// System.out.print(fibonacchi(10));
// 55
위는 내가 직접 작성한 코드고 아래는 재귀를 활용한 방법으로 구글링을 통해 알게 되었다.
조금 무식하게 작성된 코드 같아도 사실 재귀보다 반복문이 성능면에서 훨씬 유리하다.
// 재귀 활용 예시
public static int fibonacci2(int num) {
if ( num==1 ) { return 1; }
if ( num==2 ) { return 1; }
return fibonacci2(num-1)+fibonacci2(num-2);
}
나처럼 재귀적 사고에 익숙하지 않은 사람은 보자마자 머리가 띵해질 것이다.
잘 모르겠으면 그림을 그려보자.
머리가 나쁘면 몸이 고생하는 수 밖에 없다..
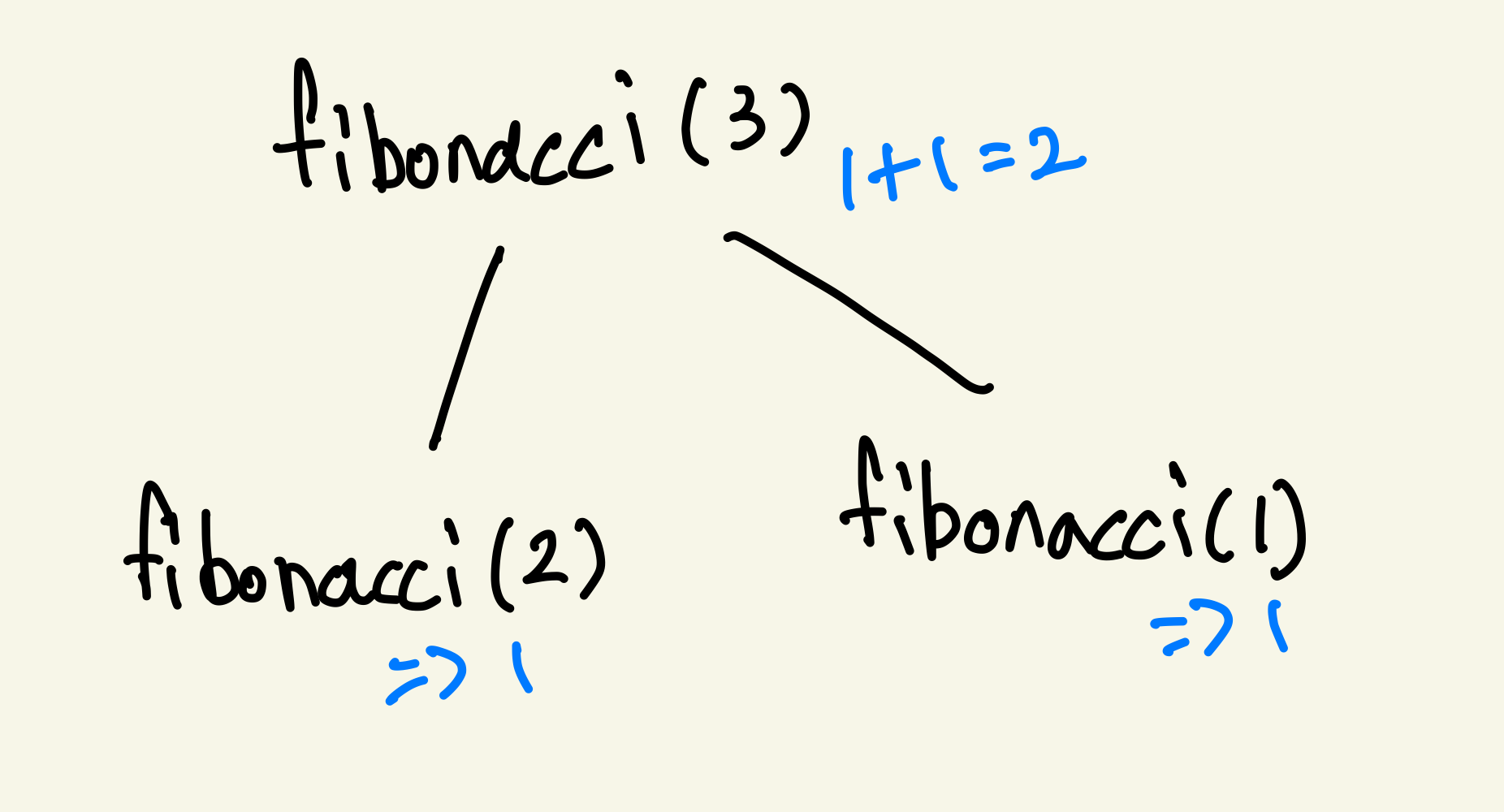
가장 간단하게 피보나치 수열의 3번째 수를 구해보자.
피보나치 수열의 1번째와 2번째가 1이라는 사실은 우리 모두 알고 있다.
그리고 피보나치의 n번째 수는 n-1 + n-2이기 때문에 피보나치의 3번째 수는 2이다.

조금 값을 키워서 fibonacci(5)를 구해보자.
만약 우리가 위의 재귀함수에 5라는 인자를 넣는다면
return fibonacci2(num-1)+fibonacci2(num-2);
// fibonacci2(4) , fibonacci2(3)
각각 fibonacci2(4), fibonacci2(3)이 호출될 것이다.
그리고 그 안에서 다시 자기 자신을 호출한다.
// fibonacci2(3)이 호출되었을 경우..
return fibonacci2(2)+fibonacci2(1);
그런데 우리는 fibonacci2 메서드의 인자가 1이나 2일 때 1을 리턴하도록 정의해놨다.
if ( num==1 ) { return 1; }
if ( num==2 ) { return 1; }
따라서 fibonacci2(3)의 안에서는 이런 일이 일어난다.
return 1+1;
이렇게 정해둔 리턴 값을 만날 때까지 끊임없이 자신을 호출한 뒤에 순차적으로 연산하며 돌아오는 것을 재귀호출이라고 한다.
반복문보다 훨씬 코드가 깔끔하고 직관적이라는 장점이 있으나 연산이 너무 복잡해진다는 것이 단점이다.
아래의 예시를 보자.

고작 피보나치 수열의 7번째 숫자를 연산하기 위해서 벌써부터 난잡하다. 그 이유는 중복된 연산을 계속해서 반복하고 있기 때문이다.
위의 예제에서 fibonacci(3)은 무려 5번이나 중복 연산되었다. 구해야할 값이 크면 클수록 이런 중복 연산은 점점 많아지고 성능은 당연히 처참해질 수 밖에 없을 것이다.
이런 문제를 해결하기 위해 등장한 것이 바로 메모이제이션(Memoization)이다.
(동일한 계산을 반복해야 할 경우 한 번 계산한 결과를 메모리에 저장해 두었다가 꺼내 씀으로써 중복 계산을 방지할 수 있게 하는 기법)
static long[] memo;
public static long fibonacci3(int num) {
if (num == 1 || num == 2) {
return 1;
} else if (memo[num] != 0) {
return memo[num];
} else {
return memo[num] = fibonacci3(num - 1) + fibonacci3(num - 2);
}이전 코드와 크게 달라진 것은 없고 고작 memo라는 배열이 하나 생겼을 뿐이다.
전혀 어려울 것이 없다.
만약 fibonacci3(10)이 처음 호출된다면 어떻게 될까?
// num에 10이 인자로 들어온다면?
public static long fibonacci3(int num) {
if (num == 1 || num == 2) { // 1, 2가 아니므로 false
return 1;
} else if (memo[num] != 0) { // memo[10]은 비어있는 인덱스이므로 기본값인 0이다.false.
return memo[num];
} else {
return memo[num] = fibonacci3(num - 1) + fibonacci3(num - 2);
// 이전과 같이 fibonacci3(8) + fibonacci3(9)를 실행하는데
// 그 결과를 memo[num]에 넣는다.
}위와 같은 원리로 이제는 fibonacci3(num)이 한 번 실행된다면 fibonacci3(num)에 대한 결과는 memo[num]에 이미 들어있으므로 중복 연산 과정을 거치지 않아도 된다.
성능 체크가 빠지면 섭섭하니까 간단하게 체크해보았다.
// 피보나치 배열에서 30번째 수를 구하는 연산
// 1회차
fibonacci1(배열) 소요시간(Millis) : 1
fibonacci2(재귀) 소요시간(Millis) : 9
fibonacci3(메모이제이션) 소요시간(Millis) : 0
// 2회차
fibonacci1(배열) 소요시간(Millis) : 2
fibonacci2(재귀) 소요시간(Millis) : 9
fibonacci3(메모이제이션) 소요시간(Millis) : 1
// 3회차
fibonacci1(배열) 소요시간(Millis) : 1
fibonacci2(재귀) 소요시간(Millis) : 7
fibonacci3(메모이제이션) 소요시간(Millis) : 0
// 4회차
fibonacci1(배열) 소요시간(Millis) : 1
fibonacci2(재귀) 소요시간(Millis) : 6
fibonacci3(메모이제이션) 소요시간(Millis) : 0
// 5회차
fibonacci1(배열) 소요시간(Millis) : 1
fibonacci2(재귀) 소요시간(Millis) : 7
fibonacci3(메모이제이션) 소요시간(Millis) : 0
메모이제이션 재귀 > 배열 > 재귀 순으로 빠른 연산 속도를 보여주는 것을 확인할 수 있었다.
'CS ﹒ Algorithm > Algorithm' 카테고리의 다른 글
| 계수 정렬(Counting sort)에 대해 알아보자 (0) | 2022.08.08 |
|---|---|
| 선형 탐색(Linear search)과 이진 탐색(Binary search)에 대해 알아보자 (Feat.JAVA) (0) | 2022.08.04 |
| 퀵 정렬(Quick Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.08.01 |
| 거품 정렬(Bubble Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.07.14 |
| 0부터 n까지의 수 중 소수 구하기 : 에라토스테네스의 체 (0) | 2022.06.24 |



