
고양이도 배울 수 있을 만큼 쉬운 선형 탐색과 이진 탐색에 대해 알아보자.
선형 검색 알고리즘
( == Sequential search algorithme, Linear serach algorithm, 순차 검색, 선형 탐색)
가장 원시적인 형태의 데이터 탐색 알고리즘이다.
이것은 리스트에서 찾으려고 하는 값을 맨 앞부터 끝까지 차례대로 찾아 나가는 것이다.
검색할 리스트의 길이가 길면 길수록 비효율적이지만 단순하여 구현이 굉장히 쉽고, 정렬되지 않은 리스트에서도 사용할 수 있다는 장점이 있다.
선형 검색은 데이터를 찾기 위해 데이터를 하나씩 모조리 검사하므로 시간 복잡도는 최악의 경우(worst) O(n)이다.
예시)
어렵게 생각할 게 전혀 없다. 그냥 임의의 배열에서 반복문으로 특정 값을 찾고자 한다면 그것이 선형 검색이다.
우리가 책에서 특정 페이지를 찾기 위해 한 장씩 넘겨가며 찾는다면 그것도 선형 탐색이다.
이진 검색 알고리즘
( == Binary search algorithm, 이진 탐색, 이분 탐색 )
오름차순으로 정렬된 리스트에서 특정 값의 위치를 찾는 알고리즘이다.
처음 중간의 값을 임의의 값을 택하여, 해당 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택하고 있다.
처음 선택한 중앙값이 만약 찾는 값보다 크다면 그 값은 새로운 최댓값이 되며, 작으면 그 값은 새로운 최솟값이 된다.
검색 원리상 정렬된 리스트에만 사용할 수 있다는 단점이 있으나, 검색이 반복될 때마다 목표 값을 찾을 확률이 두 배가 되므로 속도가 빠르다는 장점이 있다.
선형 검색은 계속해서 반으로 쪼개며 탐색하기 때문에 시간 복잡도가 최악의 경우(worst)에도 O(log n)이다. 반드시 정렬 기준이 있어야하며 정렬되어 있어야한다는 제약이 있지만, 정렬된 데이터에서는 최고의 효율을 보여준다.
예시)
우리가 총 1000페이지인 책에서 700페이지를 찾기 위해 책을 절반을 펼친 뒤 앞 페이지들은 배제하고 다시 뒷 페이지의 절반을 펼치고, 다시 나머지 반을 펼치고.. 이런 식으로 찾는다면 그것이 이진 탐색 알고리즘과 유사하다. 물론 실제로 인간은 정확하게 반 씩 펼칠수도 없을 뿐더러 선형 탐색을 섞을 수 밖에 없겠지만.
예시
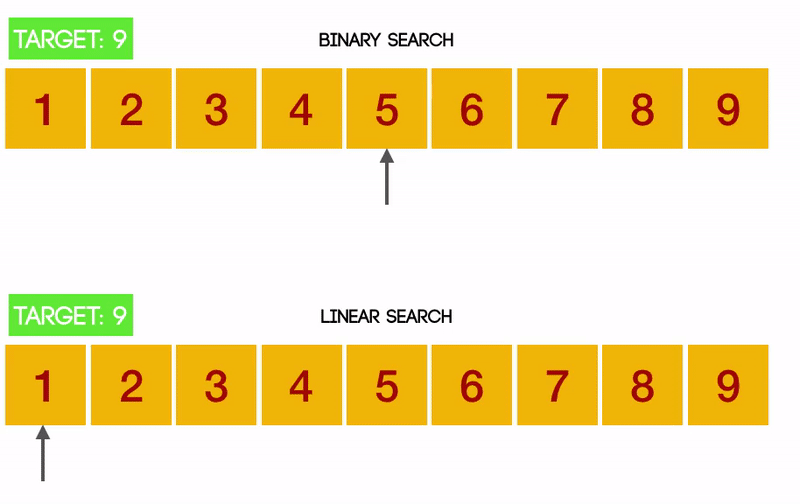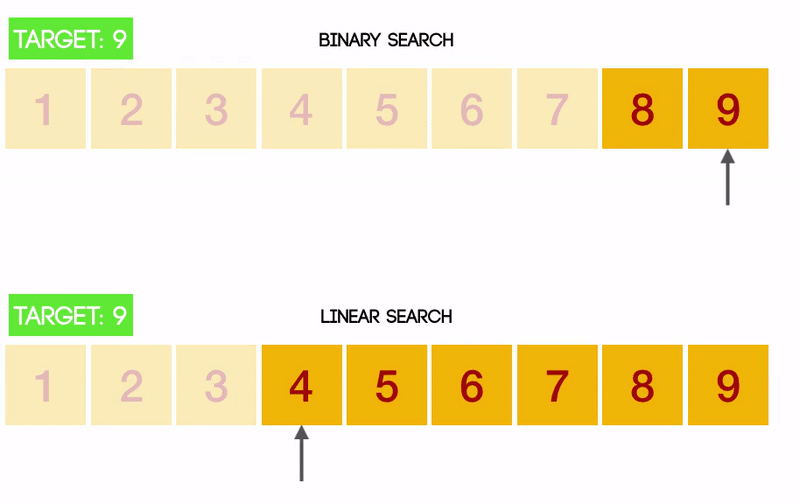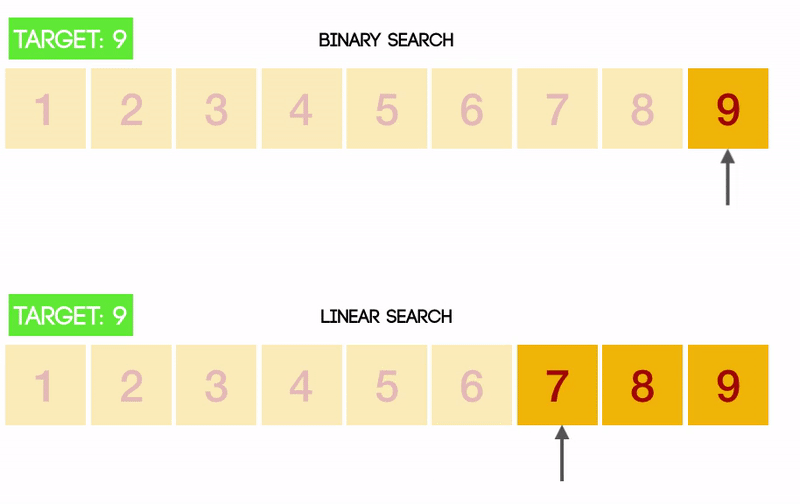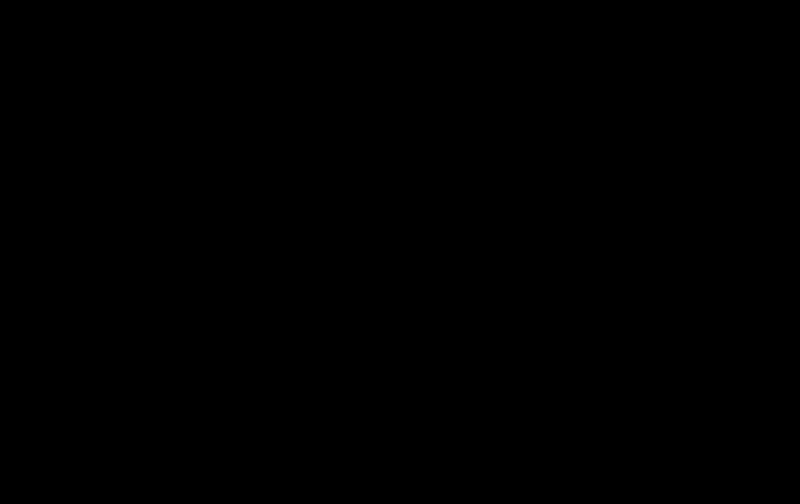
이진 탐색이 정렬만 되어있다면 얼마나 효율적인 알고리즘인지 직관적으로 알 수 있는 gif 이미지이다.
선형 탐색과 이진 탐색 둘 다에게 worst인 상황인데 차이가 엄청나다.
코드 예시
: 탐색해서 값이 있을 경우 1, 없을 경우 0을 반환하는 예시.
1. 선형 탐색
public static int linearSearch(int[] arr, int num) {
for (int n : arr) {
if ( n == num ) { return 1; }
}
return -1;
}
그냥 값이 나올 때까지 일일히 꺼내서 확인해보면 선형 탐색이다.
2. 이진 탐색
public static int binarySearch(int[] arr, int num) {
int start = 0;
int end = arr.length-1;
int mid = 0;
while ( start <= end ) {
mid = (start+end)/2;
if ( num == arr[mid] ) {
return 1;
} else if ( num > arr[mid] ) {
start = mid+1;
} else if ( num < arr[mid] ) {
end = mid-1;
}
}
return 0;
}
배열을 반으로 잘라서 찾으려는 값이 배열[절반]의 값보다 크다면 탐색 시작 위치를 [절반+1]로, 반대로 배열[절반]의 값보다 작다면 탐색이 끝나는 위치를 [절반-1]로 바꾼다.
이것을 원하는 값을 찾거나 더이상 배열을 나눌 수 없을 때까지 반복한다.
'CS ﹒ Algorithm > Algorithm' 카테고리의 다른 글
| 스윙스만큼(?) 빠른 기수 정렬(Radix Sort)에 대해 친절하게 알려드림 (0) | 2022.11.07 |
|---|---|
| 계수 정렬(Counting sort)에 대해 알아보자 (0) | 2022.08.08 |
| 퀵 정렬(Quick Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.08.01 |
| 거품 정렬(Bubble Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.07.14 |
| 피보나치 수열에서 n번째 수를 쉽게 구하는 세가지 방법. (Feat. Java) (2) | 2022.06.25 |



