
계수 정렬
( == Counting sort, 카운팅 정렬, 카운팅 소트 )
1. 계수 정렬은 비교 정렬이 아니며, 정렬할 배열의 최대값을 기준으로 새로운 배열을 만들어 값을 카운팅하여 정렬한다.
2. 계수 정렬의 시간 복잡도는 O(n)으로 일반적으로 가장 빠르다고 알려진 병합 정렬(Merge sort), 퀵 정렬(Quick sort)와 비교했을 때 우위에 있다.
3. 그러나 사실 O(n)의 시간 복잡도는 최적의 경우일 뿐이고 최대값을 기준으로 카운트할 배열을 생성하기 때문에 시간 복잡도는 최대값에 비례해서 끊임없이 높아진다. 게다가 그만한 배열을 사용하게되니 메모리 낭비는 덤이다.
4. 계수 정렬은 최대값의 제한이 없거나 너무 큰 경우에는 극도로 비효율적이고, 또한 배열 인덱스를 이용하여 카운트하는 특성상 정수만 정렬 가능하다.
예시
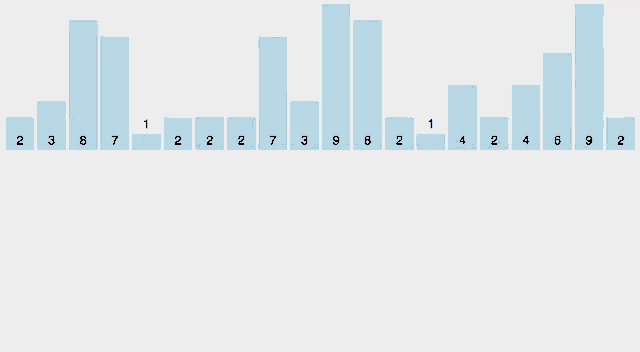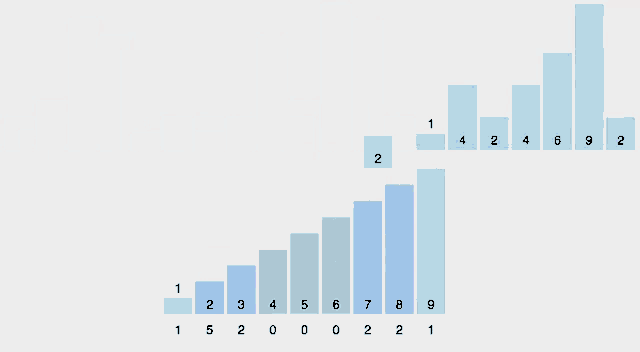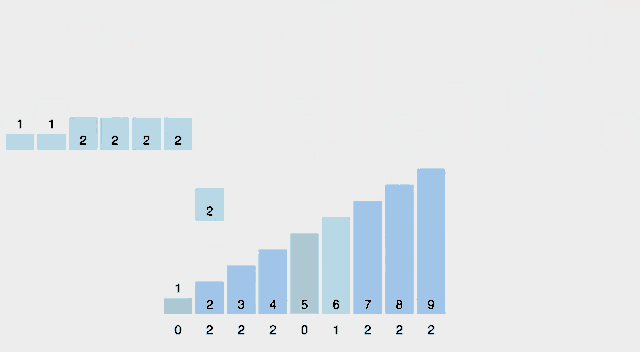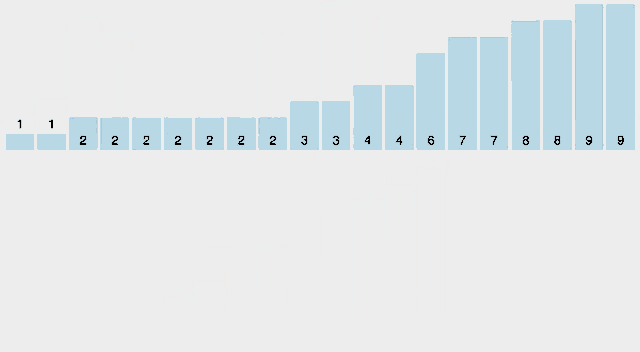
최대 값(9)의 인덱스를 가진 배열에 각 수를 카운트하여 인덱스에 수를 넣어주고 해당 배열을 토대로 정렬된 배열을 새롭게 생성하고 있다.
워낙 단순한 알고리즘이라 금방 이해가 될 것이다.
혹시나 움직이는 그림이 정신 사납다면 아래 이미지를 참고하자.
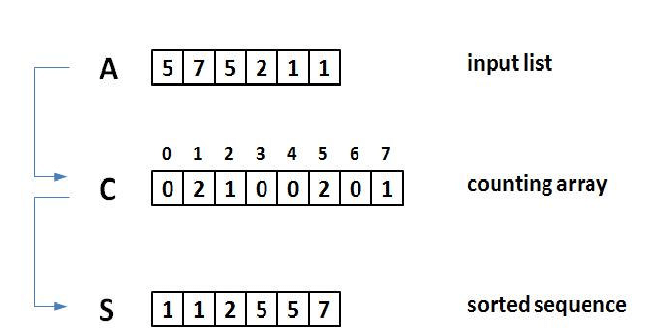
최대값이 7인 배열을 정렬할 것이기 때문에 length가 8인 배열을 생성한다.
그리고 각 값의 수만큼 대응하는 인덱스에 카운트하고, 해당 배열을 바탕으로 정렬된 새로운 배열을 생성한다.
코드 예시
: 입력 받은 임의 숫자 배열을 오름차순으로 정렬하는 예시
import java.io.BufferedReader;
import java.io.*;
import java.util.Arrays;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
int[] arr = new int[T];
// 입력 받은 값으로 배열 생성
for (int i=0; i<T; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
// 최대값
int max = Arrays.stream(arr).max().getAsInt();
int[] resultArr = new int[max+1];
// 인덱스에 중복 값 카운트
for (int i=0; i<arr.length; i++) {
resultArr[arr[i]]++;
}
// 0이 아닐 경우 (카운트 된 적이 있는 인덱스일 경우) 해당 값만큼 인덱스 넘버를 출력
for (int i=0; i< resultArr.length; i++) {
if ( resultArr[i] != 0 ) {
for (int k=0; k<resultArr[i]; k++) {
sb.append(i).append('\n');
}
}
}
System.out.println(sb);
}
}
단순히 계수 정렬만 보고 싶다면 // 인덱스 중복 값 카운트부터 읽으면 된다.
'CS ﹒ Algorithm > Algorithm' 카테고리의 다른 글
| Minumum Spanning Tree(최소 신장 트리) 구하기, 관련 문제 풀이 (0) | 2023.03.03 |
|---|---|
| 스윙스만큼(?) 빠른 기수 정렬(Radix Sort)에 대해 친절하게 알려드림 (0) | 2022.11.07 |
| 선형 탐색(Linear search)과 이진 탐색(Binary search)에 대해 알아보자 (Feat.JAVA) (0) | 2022.08.04 |
| 퀵 정렬(Quick Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.08.01 |
| 거품 정렬(Bubble Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.07.14 |



