최소 신장 트리를 구하기 위해서는 기본적으로 UnionFind 알고리즘에 대한 이해가 필요하다.
몰라도 풀 수 있지만 UnionFind를 이용하는 게 더 효율적이다.
굉장히 쉬우니까 빠르게 학습하고 오자.
UnionFind 알고리즘과 경로 압축, 그리고 관련 문제
UnionFind 알고리즘은 서로소 집합을 표현하기 위한 알고리즘이다. 일반적으로 MST(Minumum Spanning Tree)를 구할 때 사용한다. 정말 별 거 없다. 어떤 노드 6개가 있다고 가정해보자. 이 때, 1-2, 2-3, 4-5, 5-6
7357.tistory.com
MST도 쉽다. 다익스트라보다 더 쉽다.
MST란 그래프 이론에서 사용되는 개념으로, 최소한의 비용으로 모든 노드를 연결하는 그래프를 말한다.
MST를 구하기 위해서 대표적으로 사용되는 것은 Kruskal, Prim 알고리즘이다.
이름은 거창하지만 이들은 그리디 알고리즘의 일종으로, 굉장히 단순한 아이디어를 기반으로 동작한다.
여러 노드가 있고 이 노드들을 연결하기 위한 가중치가 주어질 때, 최소한의 비용으로 노드를 연결하려면 어떻게 해야 할까?
정답은 간단하다.
그냥 순서 같은 건 무시하고 가중치가 작은 Edge부터 죄다 연결하면 되는 것이다.
단, MST는 최소 비용을 구해야 하므로 당연히 노드 간에 싸이클이 형성되면 안된다.
이 싸이클 형성을 막기 위해 필요한 것이 UnionFind 알고리즘이다.
아래의 예시를 보자.
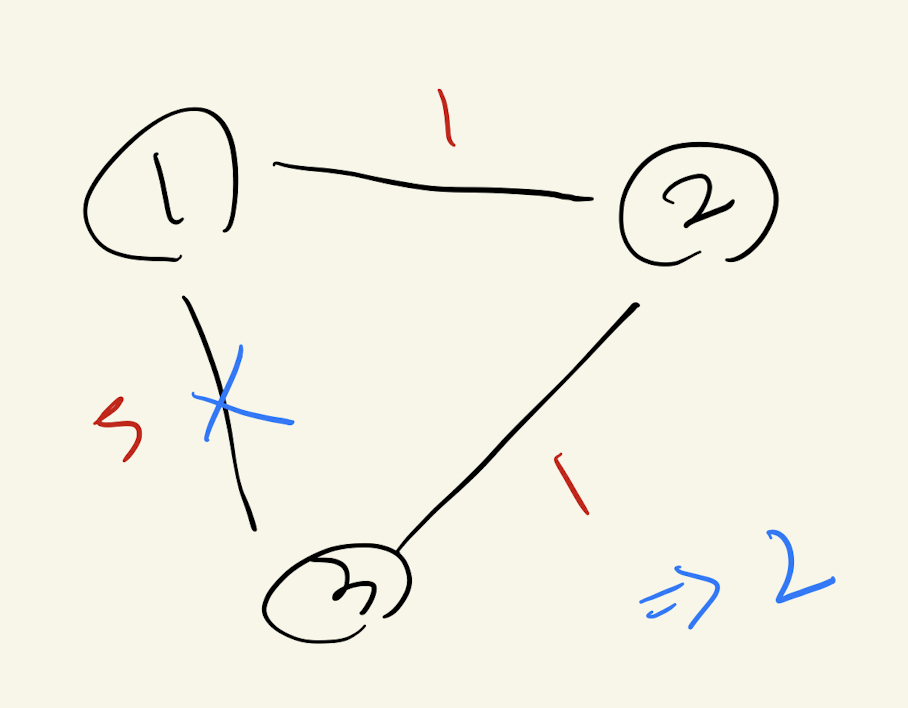
1-2, 1-3, 2-3의 가중치가 모두 2다.
그러나 무작정 이 셋을 모두 연결하게 된다면 싸이클이 형성되므로 해당 Edge 중 하나는 연결하지 않아야 한다.
따라서 Edge를 연결할 때마다 union() 연산을 통해 각 노드를 집합으로 묶어주고, 만약 find(node1), find(node2)의 값이 같다면 연결하지 않는 것이다. (즉, 둘이 같은 집합에 속해있다면)
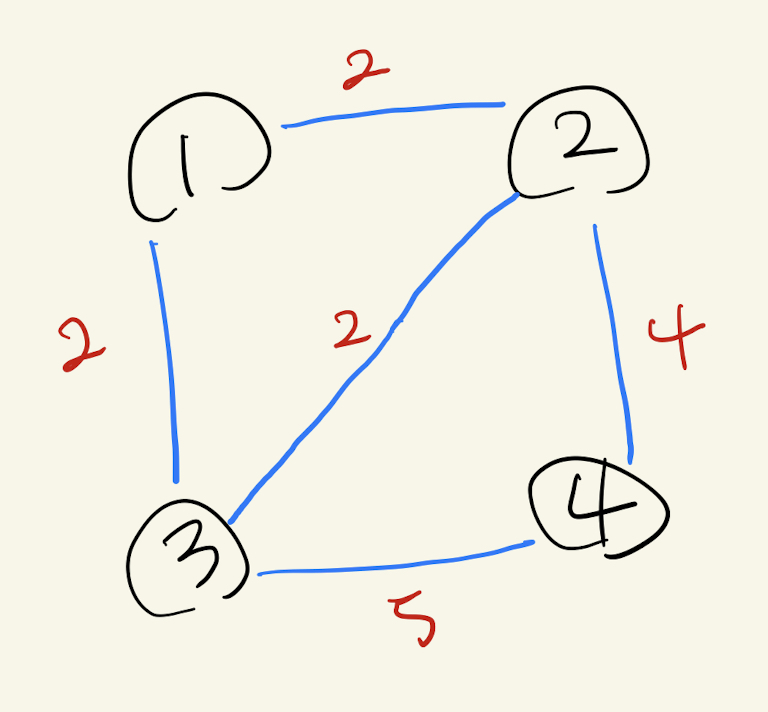
해당 규칙을 지키며 모든 Edge를 연결하게 된다면 아래와 같은 형태가 된다.

이제 Kruskal과 Prim에 대해 알아보자.
Kruskal은 Edge를 기준으로 동작하고 Prim은 Node를 기준으로 동작한다는 차이가 있을 뿐, 큰 차이는 없고 대부분의 문제는 둘 중 뭘 사용하던 문제 없이 통과할 수 있다.
(굳이 따지자면 밀집한 그래프에서는 프림 알고리즘이, 희소 그래프에서는 크루스칼 알고리즘이 더 효율적이다.)
Kruskal 알고리즘을 활용하여 MST를 구하는 순서는 다음과 같다.
1. Edge 정보를 new int[]{노드A, 노드B, 가중치} 형태로 저장한다.
2. 배열을 가중치 기준으로 정렬한다. (Priority Queue를 써도 무방하다.)
3. 배열 혹은 우선순위 큐를 순회하며 노드A, 노드B가 서로 다른 집합일 경우 (find(nodeA) != find(nodeB)), union() 연산을 수행하고 가중치를 더한다.
4. 반복문 순회가 끝나면 총 가중치가 구해진다.
코드로 확인해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
// 간선 정보를 저장할 리스트
List<Edge> edges = new ArrayList<>();
for (int i = 0; i < m; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
int w = sc.nextInt();
edges.add(new Edge(u, v, w));
}
// 가중치를 기준으로 간선을 오름차순 정렬
Collections.sort(edges);
// union, find에 대한 구현은
int cost = 0;
for (Edge edge : edges) {
int u = edge.u;
int v = edge.v;
int w = edge.w;
if (find(u, parent) != find(v, parent)) {
union(u, v, parent);
cost += w;
}
}
System.out.println(cost);
|
cs |
Prim 알고리즘을 활용하여 MST를 구하는 순서는 다음과 같다.
1. Node 정보를 new int[]{목적지, 가중치} 형태로 PriorityQueue에 가중치 기준 오름차순으로 정렬한다.
2. queue에서 Node를 가중치 순으로 뽑아내서 MST에 추가한다.
3. UnionFind를 사용하던, boolean 배열을 사용하던 해당 노드의 연결 여부를 표시한다.
4. 순회가 끝나면 총 가중치가 구해진다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
PriorityQueue<Edge> pq = new PriorityQueue<>((a, b) -> a.weight - b.weight);
int start = 0;
int weight = 0;
key[start] = 0;
pq.offer(new Edge(start, 0));
while (!pq.isEmpty()) {
int curr = pq.poll().to;
if (visited[curr]) {
continue;
}
visited[curr] = true;
weight += key[curr];
for (int i = 0; i < V; i++) {
if (graph[curr][i] != 0 && !visited[i] && graph[curr][i] < key[i]) {
key[i] = graph[curr][i];
pq.offer(new Edge(i, key[i]));
}
}
}
return weight;
|
cs |
개인적으로 Kruskal이 더 좋다.
별 이유는 없다.
여기까지 왔으면 MST는 끝이다.
이제 문제를 풀어보자.

"다른 컴퓨터를 통해서 연결이 되어 있으면 서로 통신을 할 수 있다."
"집 안에 있는 N개의 컴퓨터를 모두 서로 연결되게 하고 싶다."
"기부할 수 있는 랜선의 길이 최댓값을 구하라(=> N개의 컴퓨터를 연결할 수 있는 최단 거리를 구하라.)"
전형적인 MST 문제다.
MST 문제는 전반적으로 쉽기 때문에 각 랜선의 길이를 어떻게 처리할 것인지, 그리고 MST 문제라는 것만 파악하면 어려울 건 없다.
나의 경우 랜선의 길이는 char를 이용해 Map에 (char+i, i+1)같은 형태로 반복문 처리했다.
풀이 방법
1. 어떻게든 a~Z를 숫자로 치환할 방법을 생각해낸다.
2. 입력받은 랜선의 길이를 숫자로 변환하여 배열에 저장한다.
3. 저장한 값들을 new int[]{i, j, 가중치} 형태로 변환한다.
4. priorityQueue 혹은 sort 함수를 이용해 가중치 기준 오름차순으로 변경하고 if (find(node) != find(node)) { union() }연산을 수행한다.
5. 연결한 Edge의 가중치를 제외한 값이 정답.
정답 코드는 아래에.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
|
public class Main {
static Map<String, Integer> map = new HashMap<>();
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int countOfComputers = Integer.parseInt(br.readLine());
int[] parents = new int[countOfComputers];
initializeParents(parents);
initializeLan();
List<int[]> lanList = new ArrayList<>();
getLan(br, countOfComputers, lanList);
lanList = sortLan(lanList);
int totalOfLan = 0;
for (int[] l : lanList) {
totalOfLan += l[2];
}
for (int[] l : lanList) {
if (find(l[0], parents) != find(l[1], parents)) {
union(l[0], l[1], parents);
totalOfLan -= l[2];
}
}
int firstNetwork = 0;
for (int i=1; i<parents.length; i++) {
if (find(firstNetwork, parents) != find(i, parents)) {
System.out.println(-1);
System.exit(0);
}
}
System.out.println(totalOfLan);
}
private static List<int[]> sortLan(List<int[]> lans) {
return lans.stream()
.sorted((a,b) -> a[2] - b[2])
.collect(Collectors.toList());
}
private static void getLan(BufferedReader br, int countOfComputers, List<int[]> lans) throws IOException {
for (int i = 0; i< countOfComputers; i++) {
String input = br.readLine();
for (int j = 0; j< countOfComputers; j++) {
if (input.charAt(j) != '0') {
lans.add(new int[]{i, j, map.get(String.valueOf(input.charAt(j)))});
}
}
}
}
private static void initializeLan() {
for (int i=0; i<26; i++) {
map.put(String.valueOf((char)('a'+i)), i+1);
}
for (int i=0; i<26; i++) {
map.put(String.valueOf((char)('A'+i)), i+27);
}
}
private static void initializeParents(int[] parents) {
for (int i = 0; i< parents.length; i++) {
parents[i] = i;
}
}
private static int find(int lan, int[] parents) {
if (lan == parents[lan]) return lan;
return parents[lan] = find(parents[lan], parents);
}
private static void union(int lanA, int lanB, int[] parent) {
int parentA = parent[lanA];
int parentB = parent[lanB];
if (parentA < parentB) {
parent[parentB] = parentA;
} else {
parent[parentA] = parentB;
}
}
}
|
cs |
더 풀어보고 싶다면?
1. 다리 만들기2 (골드1, https://www.acmicpc.net/problem/17472)
- 문제 자체가 어렵진 않은데 더럽다. BSF + 완탐 + MST 문제임.
2. 최소 스패닝 트리 (골드4, https://www.acmicpc.net/problem/1197)
3. 섬 연결하기 (Level3, https://school.programmers.co.kr/learn/courses/30/lessons/42861)
- 정답 코드
(https://github.com/yangddoddi/Self_Study/commit/8b80f3d3ef38e131b59642ab695c15c8a44cc174)
'CS ﹒ Algorithm > Algorithm' 카테고리의 다른 글
| 스윙스만큼(?) 빠른 기수 정렬(Radix Sort)에 대해 친절하게 알려드림 (0) | 2022.11.07 |
|---|---|
| 계수 정렬(Counting sort)에 대해 알아보자 (0) | 2022.08.08 |
| 선형 탐색(Linear search)과 이진 탐색(Binary search)에 대해 알아보자 (Feat.JAVA) (0) | 2022.08.04 |
| 퀵 정렬(Quick Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.08.01 |
| 거품 정렬(Bubble Sort)에 대해 알아보자 (feat. JAVA) (0) | 2022.07.14 |



